Modern panel radiators are one of my favorite heat emitters. They’re easy to install, emit radiant and convective heat and have high quality powder coat finishes. They are nice in new construction and very well suited to retrofitting.

The panel in Figure 1 is about 2 feet high and 4 feet wide. You can see the two 1/2-inch PEX-AL-PEX tubes that supply it connecting at the middle of the base of the radiator. You can also see the non-electric thermostatic valve that regulates the flow rate and thus the heat output of the panel, making it an independent zone. There’s also a dual ball valve fixture at the base of the radiator that can isolate the panel from the system if ever necessary.

SHOW ME THE NUMBERS 

As is the case with many heat emitters in North America, the published data for heat output from panel radiators is based on relatively high water temperatures. The most common being an average water temperature of 180° F, and an assumed room air temperature of 68°. This makes the difference between the average water temperature in the radiator and the room air temperature 180-68 = 112°.  

This temperature difference, or ∆T is a reference condition which will eventually be used as part of the derating procedure for operation at lower water temperatures.  

In North America, it’s common to find heat output rating tables based on this 112° temperature difference. One example is shown in Figure 2. 

The black numbers are heat outputs (in Btu/h) based on the dimensions (height, width and thickness) of the radiator. The typical “thickness” dimension is based on one, two or three water plates within the panel. Note the reference conditions in the upper right.

ADJUSTING DOWNWARD

These rating tables are fine for installations where a conventional boiler operating at relatively high (but typical) water temperatures serves as the heat source. But what happens when panel radiators are installed in lower water temperature systems supplied by heat pumps or other low temperature heat sources? The short answer is their heat output decreases. But by how much?

To date, there is no American or Canadian rating standard that’s specific to panel radiators. This is where we turn to a European standard called EN442. It is widely accepted across Europe where tens of millions of panel rads are used, and provides the basis for adjusting heat outputs over a wide range of conditions. It also involves several calculations. The first of which is given as Formula 1:

Formula 1

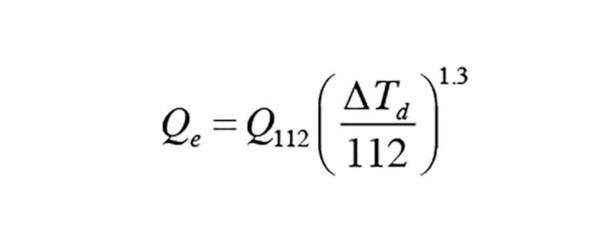
Where:

Qe = estimated heat output of the panel radiator (Btu/h)

∆Td = temperature difference determined using either Formula 2 or Formula 3 below (° F)

Q112 = the output of the panel radiator when the difference between the average water temperature and room air temperature is 112° (Btu/h)

1.3 = an exponent (not a multiplier) (use [yx] key on scientific calculator or your smart phone)

     Formula 2:

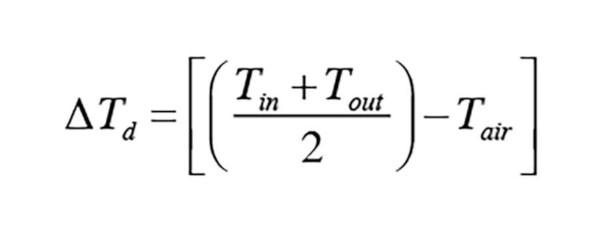
 Formula 3:

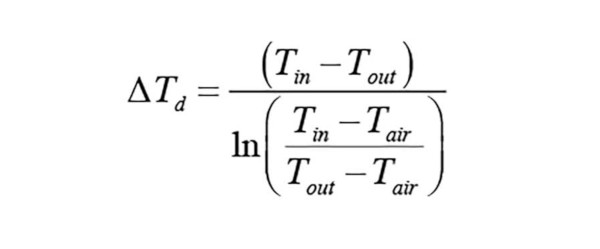
Where:

∆Td = effective temperature difference (° F)

Tin = inlet water temperature to panel (° F)

Tout = outlet water temperature from panel (° F)

Tair = room air temperature (° F)

ln = natural logarithm function (use [ln] key on scientific calculator or your smart phone)

Here’s an example:  In Figure 2, a 2-water plate radiator that’s 24 inches high and 48 inches long has a rated heat output (at ∆T= 112°) of 9,500 Btu/h. Estimate its heat output assuming an inlet water temperature of 160°, an outlet water temperature of 140° and a room air temperature of 65°.  

For now, we will use Formula 2 to calculate the value of ∆Td:

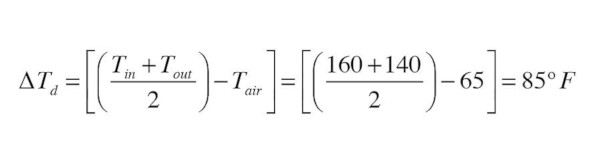
The value of Qn for Formula 1 is the radiator’s listed heat output at ∆T= 112, which was 9,500 Btu/h.

Now, just put the numbers into Formula 1 and grab your (scientific) calculator. You can use a scientific calculator to raise a number to the 1.3 power. Don’t have one? Just turn on you iPhone, press the calculator APP, and turn the phone to the “landscape” orientation — instant scientific calculator. Here’s the result.

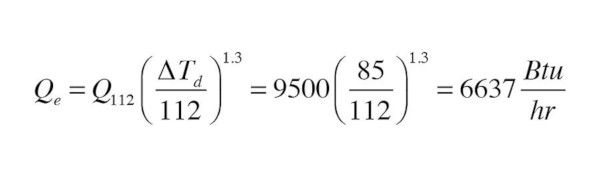
As the entering water temperature drops closer to the room air temperature, or the flow rate through the panel changes, the EN442 standard introduces a modified way to calculate the difference between the average water tempera-ture in the panel and the room air temperature (e.g., the value of ∆Td used in Formula 1). This is where Formula 3 comes in.  

The decision on using Formula 3 rather than Formula 2 is based on yet another formula (sorry, but it’s necessary). We’ll call it Formula 4.

Formula 4:

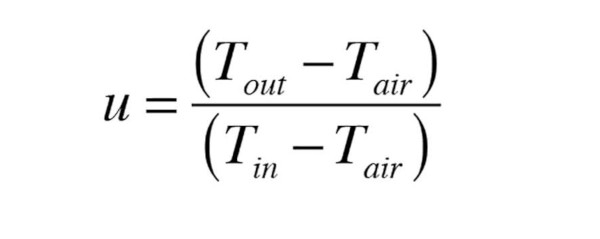
Where:

Tout = outlet fluid temperature from panel (° F)

Tin = inlet fluid temperature to panel (° F)

Tair = room air temperature (° F)

This formula looks at how the outlet temperature of the radiator is dropping relative to the inlet temperature. As the flow rate through the panel decreases there would be a wider temperature drop across the panel, and thus the value of “u” in Formula 4 will drop.

Here’s the criteria set by the EN442 standard:

• If u < 0.7, use Formula 3; and

• If u ≥ 0.7, use Formula 2.

Here’s another example. Water enters the panel radiator used in the previous example at 115°, and exits at 92°. The air temperature in the room is 65°.  Determine the correct ∆Td to use in Formula 1.

Solution: Start by calculating the value of u:

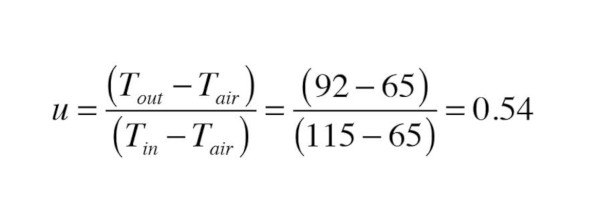
Since 0.54 < 0.7 the EN442 standard prescribes use of Formula 3 to calculate ∆Td:

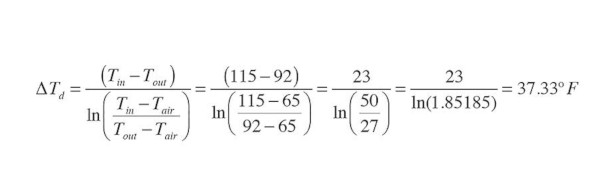
You’ll again need scientific calculator (or your iPhone turned horizontally) to get the natural logarithm [ln] of 1.85185 in the above calculation. No big deal, just enter 1.85185 on the calculator display and press the [ln x] key.

Now that the appropriate value of ∆Td has been determined, the final step is to plug the numbers into Formula 1:

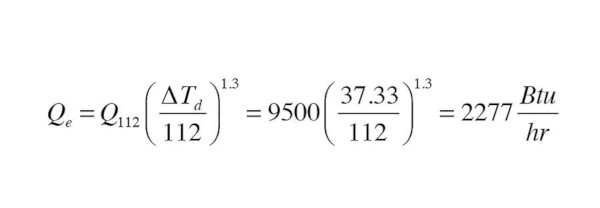
This is roughly about one quarter of the “rated” heat output of the panel. I’ve found 25% to be a good “ballpark” ratio between the published heat output ratings of most panel radiators, based on the ∆Td = 112° rating conditions, and the estimated output when operating the panels in the range of 105°-110° average water temperature.

WORKING BACKWARDS  

Now that you know how to derate the heat output of panel radiators at lower water temperatures, let’s consider a typical sizing calculation where you need to select a specific panel for a specific design load.

Consider a room with a design load of 2,500 Btu/h. The selected panel radiator will be supplied with water at 115°, and operate with a 25° temperature drop. The room temperature will be 70°.  Use the above information to select two possi-ble radiators from the table in Figure 2.

Solution: Start with Formula 4:

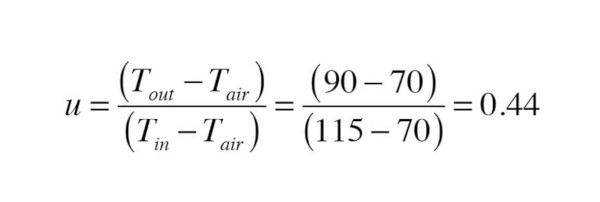
Since u < 0.7 use Formula 3 to get ∆Td:

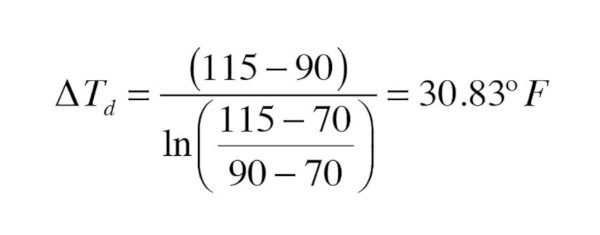
Next, set up Formula 1 with all the known information, including the required heat output at the lower water temperature (e.g., 2,500 Btu/h):

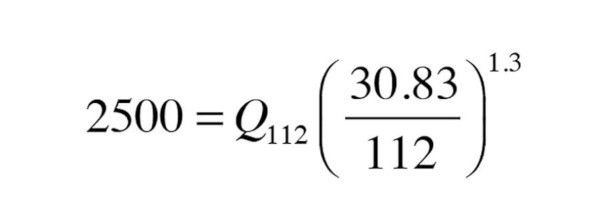
This can be solved for the necessary output at the ∆Td = 112°:

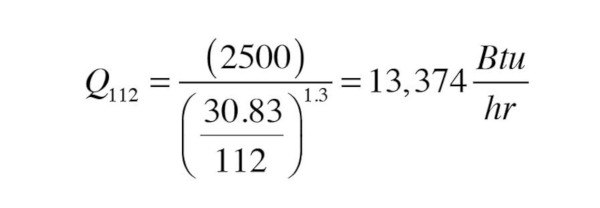
Now it’s just a matter of looking through the table in Figure 2 to find a radiator with a listed output close to this value. The three water plate (thickest) panel with a height of 24 inches and length of 48 inches has an output of 13,664 Btu/h, which is very close to calculated output. A three water plate panel that’s 20 inches high and 64 inches long has a listed output of 15,829 Btu/h — more than enough.

Thanks for hanging in there through the math. Think of these formulas like your tools. Used properly, they get you to the results you need. In this case, they give you accurate ways to select panel radiators that are compatible with low temperature hydronic heat sources like geothermal or air-to-water heat pumps. That’s a good skill to have as hydronics technology evolves.