The disproportionate world of hydronics
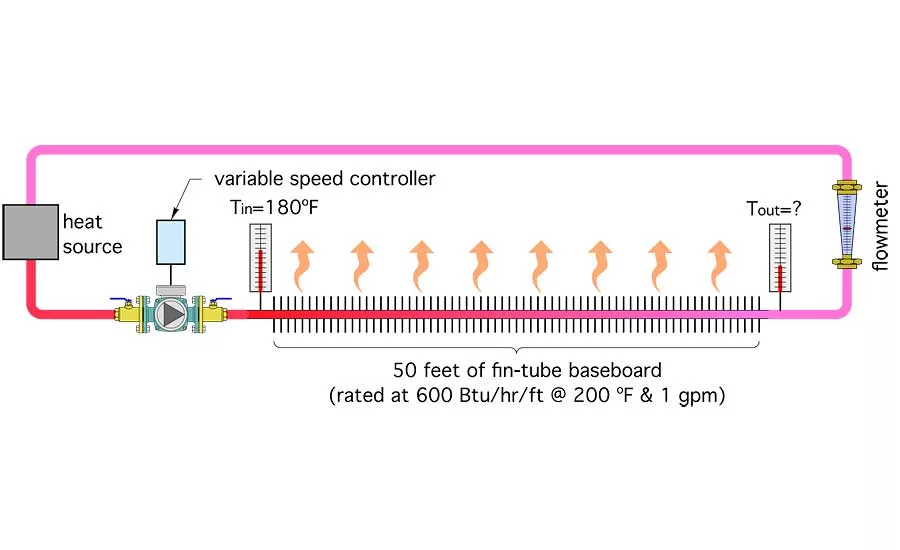
Figure 1. This circuit contains 50 feet of residential fin-tube baseboard along with a variable-speed circulator, flow meter, two temperature gauges, and a heat source. Photo credit: John Siegenthaler
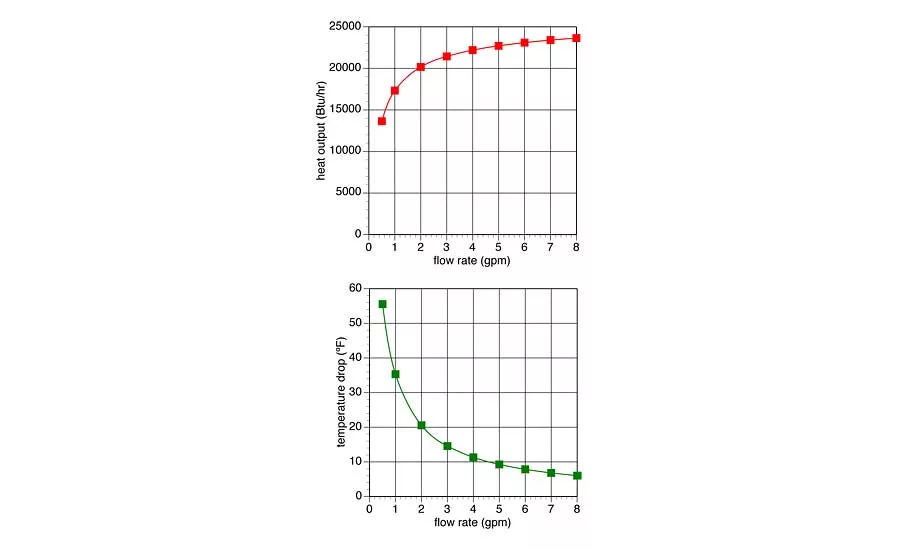
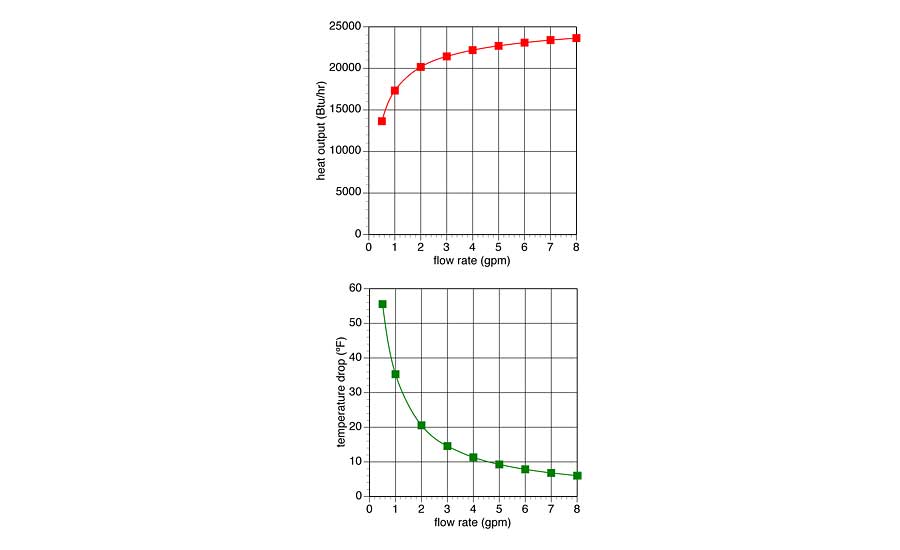
Figure 2. Graph the results for heat output and temperature drop at each of the flow rates. These graphs will look similar to the graph here. Photo credit: John Siegenthaler
When “thinking mathematically,” most people work with proportions. For example, if someone is baking brownies and wants to make a double batch, he or she intuitively knows they need to double the amount of ingredients.
So, if a person who thinks this way is told that a 100 horsepower engine, at full throttle, could make a certain car go 100 miles per hour, and then they are asked how fast a 200-hp engine would make the same car go, they’re likely to answer 200 mph.
Unfortunately, nature doesn’t always work in proportions. NASCAR fans know that it takes a lot more than 200 hp to push a race car around the track at 200 mph. With current racing technology, it takes almost 800 hp to produce that kind of speed, and most of that power goes into overcoming the aerodynamic drag of the car at those high speeds.
Some things are not proportional
Hydronics also has its share on non-proportional relationships. One of them is how the heat output and temperature drop across a heat emitter is effected by the flow rate through it.
For example, suppose a given length of residential fin-tube baseboard was yielding a heat output of 5,000 Btu/h when operating at a flow rate of 1 gpm. If asked what would happen when the flow rate is doubled, while all other conditions remained the same, most people, including some who work with this hardware every day, would say that heat output would double. That answer might seem intuitive, but it’s far from correct.
How about if the flow rate were increased from 1 to 4 gpm? That’s four times more water through the same baseboard in a given time. Surely that would at least double the heat output.
To answer this just look at some IBR output ratings from baseboard manufacturers. They’re given for a wide range of water temperatures, and for flow rates of 1 gpm and 4 gpm. You’ll find the rating at a flow rate of 4 gpm is only about 6% higher than the rating at 1 gpm, all other conditions being the same. The reason lies deep in the workings of natural convection between the water and inside tube wall of the baseboard. The theory is complex, but the results are simply how nature behaves.
Taking some measurements
Suppose you made up a hydronic circuit like the one shown in Figure 1.
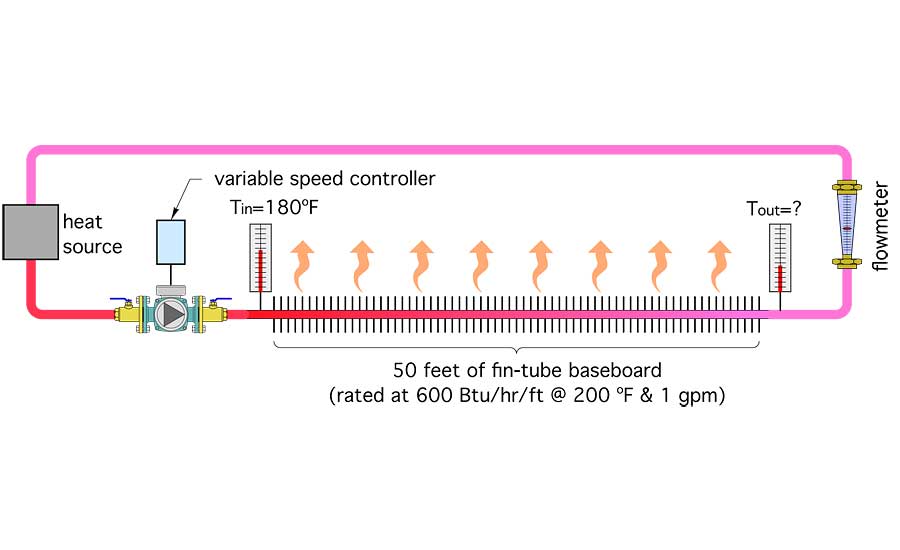 This circuit contains 50 feet of residential fin-tube baseboard along with a variable-speed circulator, flow meter, two temperature gauges, and a heat source. Assume that the heat source is controlled so that the supply water temperature into the fin-tube element stays at 180° F.
This circuit contains 50 feet of residential fin-tube baseboard along with a variable-speed circulator, flow meter, two temperature gauges, and a heat source. Assume that the heat source is controlled so that the supply water temperature into the fin-tube element stays at 180° F.
You turn on the circulator at full speed, and the flow meter reads 8 gpm. The inlet temperature is steady at 180°, and in a short time the outlet temperature of the fin-tube element stabilizes at 174°. Knowing the flow rate and temperature drop along the fin-tube, you can calculate the rate of heat dissipation as follows:
q = (8.01Dc)(ƒ)(∆T) = (8.01 x 61.3 x 1.00)(8)(180-174) = 23,570 Btu/h
Where:
q = rate of heat output (Btu/h)
D = density of the fluid (lb/ft3)
c = specific heat of fluid (Btu/lb/°F)
ƒ = flow rate (gpm)
∆T = temperature drop (°F)
8.01 = a number that makes the units correct
Now that you have a reasonable measurement of the heat output at a flow rate of 8 gpm, you reduce the speed of the circulator so that the flow rate drops by 1 gpm, wait for temperatures to stabilize again, and write down the measured flow rate and outlet temperature. You keep repeating this procedure for flow rates all the way down to 0.5 gpm. Then, you use these data for flow rate and temperature drop to calculate the heat output rate from the baseboard.
After you’ve done all this, you graph the results for heat output and temperature drop at each of the flow rates. These graphs will look similar to the graph in Figure 2.
Far from proportional
The graph of heat output from the baseboard versus flow rate is probably not what you expected — especially if you think proportionally. It shows that heat output from the fin-tube element drops off rather slowly with decreasing flow rate until you get down to a flow rate of about 2 gpm. Below this value, heat output starts to drop off more rapidly with decreasing flow rate.
Although it might not be what you expected, it is what it is. This characteristic is shared by all hydronic heat emitters — fin-tube, convectors, panel radiators, and even radiant panel circuits. Heat output changes very quickly at low flow rates but very gradually at higher flow rates. This trend also holds true at other supply-water temperatures.
The graph of temperature drop versus circuit flow rate shows that ∆T is anything but constant. The ∆T happens to be at the commonly assumed value of 20° when the flow rate is a bit over 2 gpm. As flow increases above 2 gpm, the ∆T keeps dropping. At 8 gpm it’s only about 6°. If the flow through the baseboard was only 0.5 gpm, the ∆T is slightly above 55°.
These ∆T values are the direct result of heat output. There’s nothing in this setup that constrains the ∆T to stay at any particular value. There’s also nothing “wrong” with the fact that ∆T is changing. It just goes where nature takes it as we stand by and watch.
A ‘score’ for hydronics
When Abraham Lincoln began his Gettysburg address in 1863 with the words, “Four score and seven years ago,” he was referring to 1776, the year when the Declaration of Independence was signed. If you do the math, 1863 – 1776 = 87. Now, take that difference in years, subtract 7, and divide by 4. You’ll arrive at the conclusion that a “score” refers to 20 years.
So what has this got to do with hydronics? Not much other than the number 20. Over the years I’ve been amazed at the unwavering faith that many North American hydronic heating professionals have to this number. Some just assume that every hydronic heating circuit “knows” to operate with a 20° ∆T. It’s as if the water in the system has been “programmed” to operate at a 20° drop. This is obviously not true, and it’s also not necessary.
In Europe it’s common for panel radiator circuits designed for load temperature drops of 30°-36°. They do this because it reduces flow rate, and reduced flow rate means small pipes and small circulators. It also means lower operating cost. Over there, electricity is expensive and every watt counts. They won’t operate a circulator at 45 W, if it can create the necessary heat transfer while operating at 20 W. They care, and so should we.
Radiant floor-heating circuits can also be designed for different design load ∆Ts. I like to design around 15° for floor circuits in areas that are expected to have “barefoot-friendly” floors. The smaller ∆T reduces variation in floor surface temperature a bit compared to what it would be at a ∆T of 20°. However, in an industrial building, I may push the design load ∆T for the circuit up to 25°. That’s because heated concrete slabs in most industrial building don’t need to be “barefoot friendly.” Slightly wider variations in floor surface temperature are hard to notice through a pair of work boots. Designing around slightly larger circuit temperature drops also reduces flow rate, which in turn decrease circulator size and power requirements.
It’s not a constant
It’s also important to understand that the ∆T of a circuit decreases when the supply water temperature decreases. In any system where the water temperature is regulated based on outdoor reset control, the supply water temperature decreases as the outdoor temperature increases. As the supply temperature drops, and the flow rate through the circuit remains constant, the ∆T of the circuit must drop. If it didn’t the multiplication of flow rate x ∆T would remain constant, and this would imply the same rate of heat output regardless of the supply water temperature.
The math associated with assuming a fixed ∆T of 20° works:
Q = 500 x (1 gpm) x (180° - 160°) = 10,000 Btu/h
Q = 500 x (1 gpm) x (100° - 80°) = 10,000 Btu/h
Funny how the math associated with some of our assumptions can lead to incorrect conclusions — conclusions that are mathematically correct, but way off when it comes to physics. In this case, assuming that the ∆T remains constant at 20° regardless of the supply water temperature implies that the latter is irrelevant.
As long as we assume the water temperature drops 20° through the circuit, and we maintain the same flow rate, the supply water temperature could be anything and we would get the same heat output. If you want to believe that math supersedes physics, try turning down the aquastat on a boiler supplying a typical baseboard system from 180° to say 100° and wait to see what happens when the weather turns cold.
Only from the rhine
Frustration can lead to sarcasm. During training sessions I used to joke about getting water from the Rhine River in Germany for use in North American hydronic systems. The pitch was that the German’s are so smart they’ve trained the water in the Rhine to drop 20° if it ever finds itself in a North American hydronic heating system. Most people quickly figured out this was a ruse. Still, when someone later comes up and whispers in my ear: “Hey, how can I rep that German water?” I realize there’s opportunity for more discussion.
The relationship between the heat output of a hydronic circuit and the flow rate passing through it is not proportional. Neither is the relationship between the circuit’s temperature drop and the flow rate through it. Be sure to examine this relationship as you design future systems. Opportunities abound for reducing installation and operating costs based on reduced flow rates and higher circuit temperature drops. The number 20 is not sacrosanct.
To read Siegenthaler’s article in pdf form, please see here.
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!







