Heat pumps are incredibly useful devices. They gather what would otherwise be unusable heat from low temperature sources such as outside air, soil, lakes or water wells and “upgrade” the temperature of that heat to a condition where it can heat buildings, domestic water, swimming pools or other process loads.

As the global taste for fossil fuels continues to “sour,” electrically-powered heat pumps will continue to gain market share as heat sources.

One of the areas in which this is already occurring is residential domestic water heating. Federal regulations that went into effect in 2015 require electrically-powered storage water heaters having 12 kW or less of power input, and volumes more than 55 gallons, to use heat pump technology. 
This mandate spawned many products that, in essence, combine a small air-to-water heat pump assembly with an insulated DHW storage tank. Most commercially available products in this category mount the heat pump components on top of and attached to the thermal storage tank, as illustrated in Figure 1.

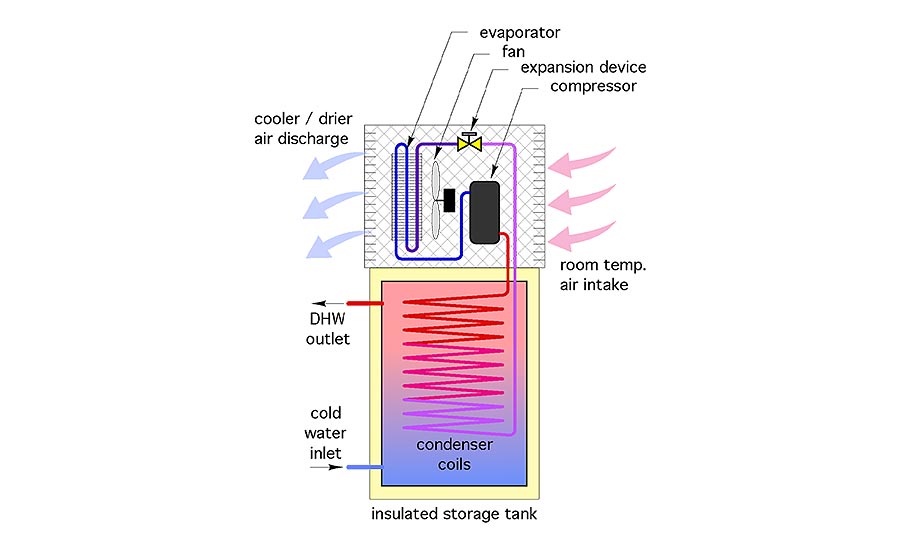
The heat pump assembly pulls room air across its evaporator coil, extracting heat from it, and in some cases, condensing water vapor in the air. The cooler and drier air discharges into the surrounding space. Refrigerant flows from the evaporator coil to the compressor where its temperature and pressure are increased. The hot refrigerant gas passes through condenser coils located in the tank, or wrapped around the perimeter of the tank under the insulation. Heat moves from the condenser coils into the domestic water. The refrigerant condenses back to a liquid as it gives up heat. It then flows to an expansion device where its temperature and pressure are lowered to a condition allowing the cycle to continue. This basic, non-reversible refrigeration cycle is used in millions of devices like refrigerators, room air conditioners and water coolers.

Use where appropriate  

Heat pump water heaters make a lot of sense when they can be located in areas that have a surplus of heat. Examples would include a garage in a southern climate or a space filled with equipment that generates heat. They can also keep a basement cooler and drier during humid summer weather. Most heat pump water heaters do not have sufficient cooling capacity or a means of air distribution to make them practical for whole house cooling.

One application I’ve heard proposed several times involves locating a heat pump water heater in a house that uses a separate heat pump for heating, and possibly for cooling. This concept sets up some interesting thermodynamics.   

The house heating heat pump would absorb free heat from its source, e.g., outside air, geothermal loop, etc. Additional energy in the form of electricity is added to this absorbed heat in the process of increasing its temperature. The heat used to maintain comfort in the building is thus partially “free” heat and partially “paid for” heat. The higher the heat pump’s coefficient of performance (COP), the greater the ratio of total heat divided by “paid for” heat. 

The heat pump water heater absorbs some of this combined “free” plus “paid for” heat, and adds more “paid for” heat (e.g., electricity) to push the temperature of the heat high enough to be absorbed into the domestic water. The heat that makes it into the domestic water is therefore a combination of “free heat” and some “paid for” heat at the first heat pump, and more “paid for” heat at the heat pump water heater. Figure 2 illustrates the concept.

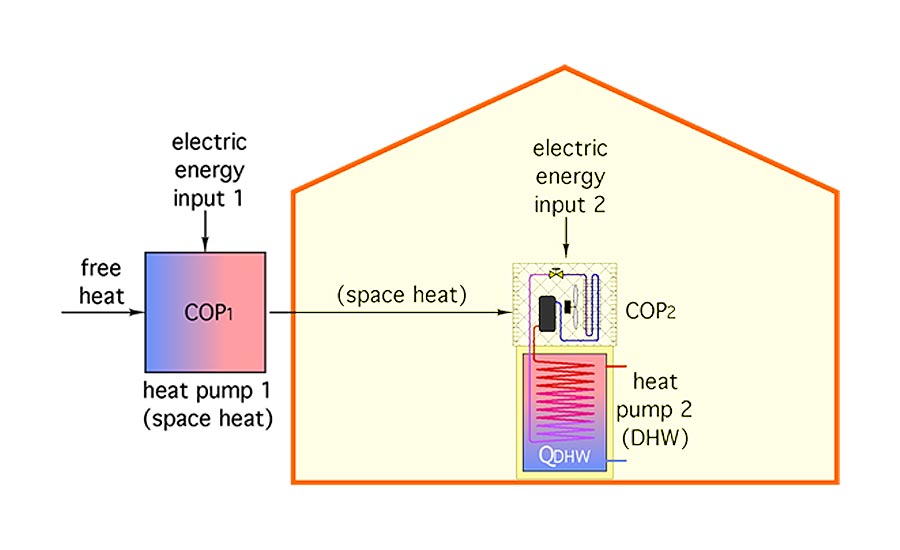
So what’s the net effect of this energy flowing through two cascading heat pumps? It could be expressed as a “net” COP, which is the ratio of heat delivered into the domestic water divided by the total electrical energy used to make that happen. 

I wanted to see if a relationship could be developed for this situation based on the COPs of the two cascading heat pumps.  After sketching out formulas based on the fundamental thermodynamic concepts, I reduced it down to Formula 1, shown below.

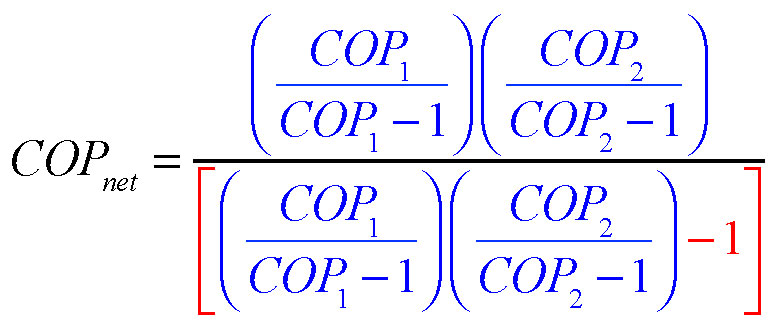
Where:
COPₙₑₜ = the effective COP of the overall process based on the heat added to the domestic water and the total electrical energy needed to make that happen;
COP₁ = the nominal COP of the space heating heat pump; and
COP₂ = the nominal COP of the heat pump water heater.

Some of you are probably looking at this formula as being really complex. But look closer: The part of the formula shown in blue is the same in the top (numerator) and bottom (denominator).  You only have to calculate it once. Then just subtract 1 from this calculation for the denominator.

Let’s run some numbers to see how this works. Consider an installation where the heat pump that supplies space heating is operating at a COP₁ of 4.0. The heat pump water heater is operating at a COP₂ of 3.0. The net COP based on getting free heat into domestic water would be:

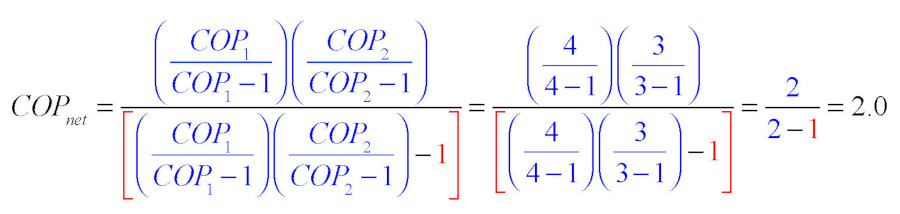
This result can be interpreted as follows: For every two units of heat added to domestic water, one came in the form of “free” heat, and the other came in the form of “paid for” electrical energy. Even though the net COP of 2.0 is significantly lower than the stated COP of the heat pump water heater (e.g., 3.0), the water is being heated using one half of the electrical energy that would be required by any type of electric resistance heating device.

Let’s run another set of numbers assuming very high COPs for both heat pumps. Assume the space heating heat pump was operating at a COP₁ of 5.0, and the heat pump water heater was operating at a COP₂ of 4.5. Putting these numbers into the formula yields the following:

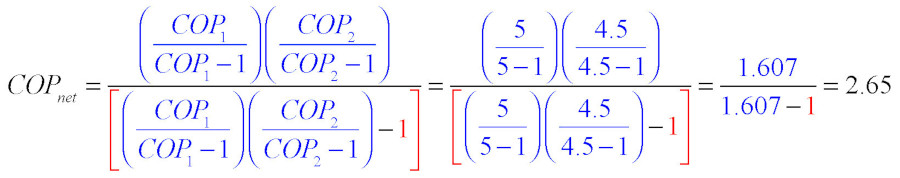
The net COP is going up — as it should — but it’s still substantially lower than the “stand alone” COP of the heat pump water heater (e.g., 4.5).

One mathematical caution is in order. Dividing by 0 is undefined. This implies that Formula 1 is only valid when both COPs are greater than 1.0.  

So what would happen if both heat pumps had a very low COP of 1.01?  I’ll spare you the number crunch, but the result is a net COP of 1.000098, just a tiny bit better than full electric resistance heating, and certainly not worth the mechanical complexity of using two heat pumps.

Another viewpoint

The net COP as calculated above is defined as follows:

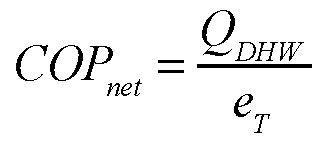
Where:
QDHW = energy transferred to domestic water; and
eT = total electrical energy used to move “free” heat into domestic water.

This definition is consistent with how heat pump COPs are defined (e.g., heat output rate divided by electrical input rate), but there are other ways to look at the situation. One would be a ratio of the “free” heat divided by the total heat supplied to the domestic water, which can be calculated using Formula 2.

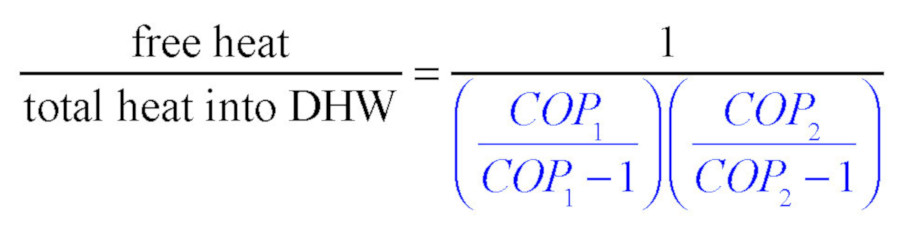
Where:
COP₁ = the nominal COP of the space heating heat pump; and
COP₂ = the nominal COP of the heat pump water heater.

Let’s again assume very high COPs for the two heat pumps — 5.0 for the space heating heat pump and 4.5 for the heat pump water heater. Plugging these numbers into Formula 2 yields the following:

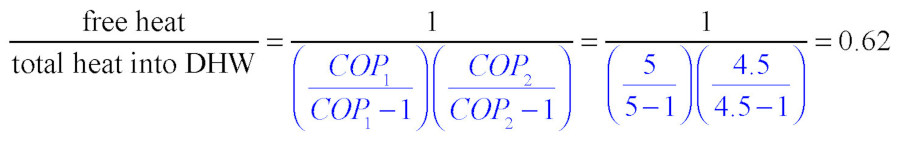
This means 62% of the energy added to the domestic water was free energy, while the other 38% was “paid for” electrical energy.

When this doesn’t apply  

These calculations just discussed assume that all the energy absorbed by the heat pump water heater came through the heat pump supplying space heating. There will definitely be times when this assumption doesn’t apply. One would be heat from solar gains. Another would be internal heat gains from occupants, stoves, ovens, hair dryers, computers, lights, toasters, entertainment equipment and exercise equipment. Yet another would be heat added to the building by conduction and air leakage during warm weather. In such cases, the “stand alone” COP of the heat pump water heater would apply. 

An annual average COP for the heat pump water heater would have to combine the effect of heat added to the building by the space heating heat pump, and that added by all other internal heat gains. In all cases, this would increase the net COP of the heat pump water heater in comparison to the numbers predicted by Formula 1, and the ratio of “free” heat to total heat predicted by Formula 2. 

A final idea worthy of more investigation is a performance comparison between using the cascading heat pump scenario just described versus providing the majority of the domestic water heating load using a heat exchanger and a buffer tank. The heat exchanger could be a coil within the buffer tank, or an external brazed plate unit. Heat from the same heat pump that provides space heating would maintain the buffer tank at a setpoint temperature or temperatures based on outdoor reset control. The majority of the domestic water heating temperature lift would come from the heat exchanger. Any further temperature lift would come from either a tankless or tank-type electric water heater. 

My suspicion is that the net COP of this approach would be higher than that of the cascading heat pumps, especially in situations where the majority of the heat for the heat pump water heater was provided by the space heating heat pump. Drilling down into this idea is on my to-do list. Stay tuned.