This month I want to deviate a bit from a purely renewable energy topic to one that’s important across the entire spectrum of hydronics technology. It’s a topic that likely gets exercised on a daily basis in any engineering office where water-based HVAC systems are conceived.
Those who have worked with the technical side of hydronics have likely used terms such as: Pressure, differential pressure, head and head loss. These terms all have legitimate and specific meanings. But when some of these words get scrambled into jargon, the result can be an undefined or meaningless term. One example of such a scramble is “head pressure.”
To see why the phrase “head pressure” is not a valid technical term, it’s important to understand both words.
Let’s start with head. Although I don’t know who coined this word for use in fluid mechanics, I do know where the concept that the word represents came from. It’s attributable to a man named Daniel Bernoulli. In 1738, he published a book entitled “Hydrodynamica,” which presented a concept that is now embodied in what’s appropriately called Bernoulli’s equation. Anyone who has studied fluid mechanics has surely come across this equation. It provides the basis for analyzing a wide range of situations, such as a pipeline carrying water from a reservoir to a city to the shape of airplane wings to — you guessed it — fluid flow in hydronic systems.
Fundamentally, Bernoulli’s equation describes the mechanical energy present in a fluid and how that energy can be transformed as the fluid changes height, pressure and speed. The “head” of a fluid is simply the total mechanical energy contained in that fluid.
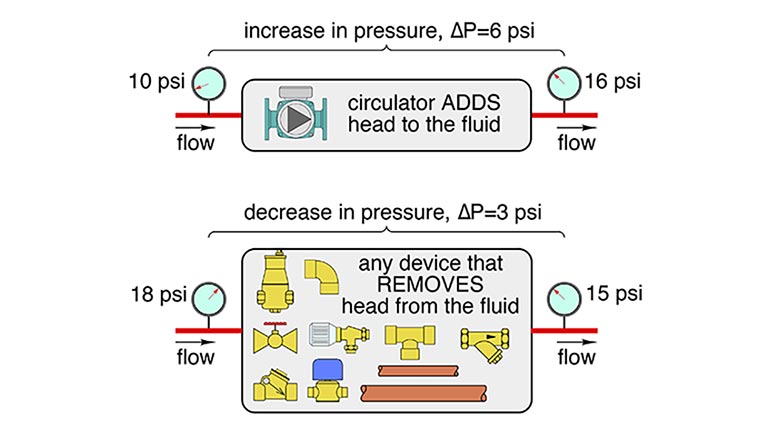
In the case of a closed-loop hydronic system, head energy is added to the fluid by a circulator. Everything else the fluid flows through — piping, fittings, valves, heat emitters, etc. — removes head energy from the fluid due to the friction present between moving fluid molecules, as well as between those molecules and the surfaces they come in contact with. This concept is illustrated in Figure 1.
Invisible but real
We can’t “see” energy. We can’t see it with our bare eyes, or under a microscope. Think about it — have you ever seen a Btu, a Kilowatt•hour or a Joule of energy?
Neither have I.
Although we can’t see it directly, we can still detect when energy is added to or removed from a material. For example, consider water flowing into a boiler at 140° F, and leaving that boiler at 155° F. If the piping into and out of the boiler were transparent, the water coming out would look identical to the water going in. Yet we know there’s more thermal energy in 155° water compared to 140°. The indicator of that additional thermal energy is a temperature rise. When thermal energy is added to a material (and the material doesn’t change phase between being a solid, liquid or gas), the temperature of that material increases. Conversely, when thermal energy is removed from a material, and the material remains in the same phase, its temperature decreases. Thus, a change in temperature is the “evidence” that thermal energy, which we can’t directly see — has been added to or removed from the material.
When it comes to head energy and pressure, there’s an analogy to the relationship between thermal energy and temperature. A decrease in pressure along a horizontal piping path is the “evidence” that head energy has been removed from a liquid. An increase in pressure is the “evidence” that head energy has been added to the liquid. We can’t see head energy, but we can detect it being added or removed from a liquid by measuring changes in pressure. The constraint of a horizontal piping path in the above statement is to eliminate any pressure change in the fluid due to elevation change. The drop in pressure due to head loss is still present in non-horizontal piping, but it would not reveal itself as the “sole” cause of the pressure difference between two points along a pipe.
Why feet?
In North America, the unit used to express head energy is “feet.” The word “feet” has undoubtedly caused a lot of confusion over the years. I know it confused me for a while. Why would energy be expressed in units that are commonly used for distance? Here again, past practices have prevailed.
The unit of feet, abbreviated as ft. comes from a mathematical simplification of the units shown in Figure 2.
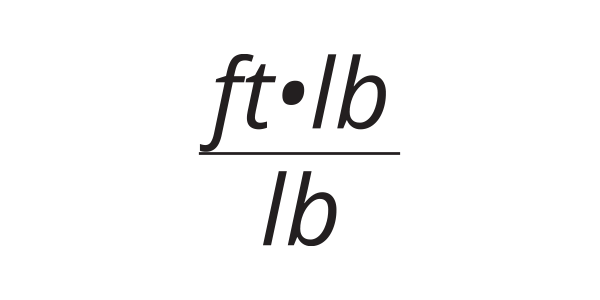
This arrangement of units would be properly stated as “foot-pounds per pound.”
The unit foot-pound, abbreviated as ft•lb is a valid unit of energy. As such, it can be converted into any other valid unit of energy. For example: 1 ft•lb = 0.0012850675 Btu.
Consider water flowing through an operating circulator. In this situation, the arrangement of units in Figure 2 can be interpreted as the number of ft•lb of mechanical energy added to each pound of water passing through the circulator. Thus, a circulator that happens to be operating at say 10 feet of head is adding 10 ft•lb of mechanical energy to each pound of water passing through the circulator.
So why don’t we say it that way (e.g., the circulator is adding 10 ft•lb of mechanical energy to each pound of water passing through it?) It’s because mathematically, the units of lb in the top of the fraction of Figure 2 cancels out with the unit of lb in the bottom of the fraction, and thus the only remaining unit is ft. It’s shorter to just state head in feet rather than fl•lb/lb.
If I had a seat at the table when this simplification became the “standard” in the industry, probably back sometime in the 1800s, my vote would have been to keep it ft•lb/lb. It’s longer, but it better represents the concept of energy per unit weight of liquid.
The relationship
So how does one determine the amount of head energy added or removed from a fluid based on observed change in pressure? Answer: Use Formula 1:
Formula 1:
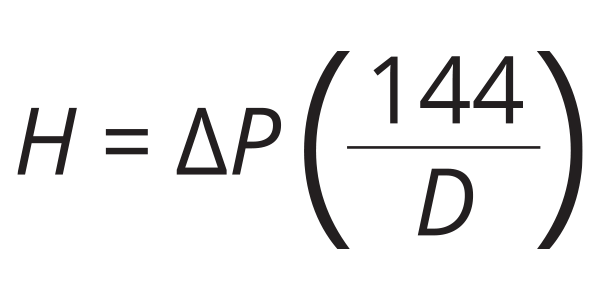
Where:
H = head (added or removed) in units of (feet);
∆P = change in pressure in units of (psi);
D = density of the fluid in units of (lb/ft3); and
144 = a number needed for the units to work correctly.
Formula 1 can be used to calculate the head energy added to the fluid when a pressure increase occurs — such as a pressure increase measured across an operating circulator. The formula can also be used to calculate the head energy removed from the fluid when a pressure decrease occurs, such as across any component or group of components connected together in the circuit.
Water at 60° F has a density of about 62.4 lb/ft3. This makes the fraction of (144/62.4) equal to approximately 2.31. However, the density of water changes significantly with temperature. The density of other liquids, such as solutions of glycol-based antifreeze, is also different from that of water, and also dependent on fluid temperature. Thus, stating that the head energy exchanged is 2.31 times the pressure change is only an approximation. It gets you in the ballpark, but the best accuracy is still attained when you use Formula 1 along with the density of the fluid. In a hydronic circuit, you can determine the density based on the average temperature of the liquid flowing through that circuit.
Slinging slang
So back to the jargon of head pressure. Based on what we just discussed, these two words, paired together, are analogous to heat temperature, a term that has no meaning in our industry, or any other industry.
Our industry uses plenty of jargon. For example, we might say that the output of a boiler is 80,000 Btu, when what we mean is 80,000 Btu/h. We might state that the electrical energy used by a small circulator is 50 watts, when what we really mean is that the power demand of the circulator is 50 watts. We may describe a circulator operating with a head pressure of 10 feet when what we mean is a head of 10 feet.
Jargon is usually acceptable, and perhaps even a bit “admirable” when describing hardware. For example, how many mere mortals know what is meant by a blind flange, street ell or bullhead tee?
However, when learning to manage the physics that determines how the system operates, jargon often clouds understanding. That leads to uncertainty, lowered confidence and even finger crossing when making design decisions. We’ve all been there at times, and it makes us (or should make us) uncomfortable.
After reading this, some may be thinking that I’m “nitpicking” about words that most of us already sort of understand. Why not be specific and take away the words “sort of” in the previous sentence. It’s precise and professional.
