Guest Editorial | David Beal
Applying the Water Demand Calculator: Public fixtures in multi-family buildings
Calculating flow rates can be tricky.

Lead image courtesy of moxumbic / iStock / Getty Images Plus.
While the IAPMO Water Demand Calculator (WDC) has been a boon for reducing pipe and equipment sizes in apartment buildings, it has faced some difficulties in application due to some notable exclusions from its documentation and calculations. Specifically, fixtures that serve apartments’ outdoor, common, or amenity spaces. These spaces have been increasingly popular in luxury apartment buildings which are vying for high-paying tenants.
This exclusion is entirely reasonable, as the original data from which the WDC is based, was conducted on single-family homes, which don’t have these spaces, and even on the larger buildings they have compared with these spaces make up such a small part of their load that they will be nearly impossible to parse out from the larger building. Unfortunately, this leaves engineers in a difficult place, as jurisdictions do still expect for pipe sizing to account for these fixtures.
For lack of better information, many jurisdictions will request that engineers calculate these public fixtures separately with Hunter’s curve and then add them to the WDC values. This can lead to very large, and often somewhat nonsensical flows (such as a single lavatory with a 0.5 gpm aerator having a 1.75 gpm of flow). Even more concerned jurisdictions might simply ask the engineer to sum the flow rate of each of these fixtures without any diversification. These can lead to small buildings sometimes doubling their WDC flow estimate with public fixtures.
Fortunately, while the WDC does not provide much guidance for their use, their calculator does provide three spaces for “other” fixtures. For these, one simply needs a flow rate and a probability. Flow rates are fairly easy to obtain, for faucets typically being stated, and for other fixtures, typical values can be found with a little searching. Probability however is a more difficult concern which warrants a far larger discussion that I intend to expound on more in a later article. However, for this article I shall focus a greatly simplified explanation.
Assuming fixture driven probability the probability formula is fairly simple P = N * t / T where P is the final probability, N is the number of operations in period T, t is the duration of a single operation in seconds, and T is the peak hour (generally between 7am-8am, in seconds) or a longer period if the probability remains uniform throughout and encompasses the peak hour (that is to say, something which has its operation independent of other building uses, such as a trash washdown).
Let us consider a few examples, first let us consider a public tank water closet. This will have a flowrate of around 3.5 gallons per operation, and taking its flush volume divided by that flow rate, we find an operation time of around 22 seconds. The remainder for this case is more difficult, as it turns out how many times this fixture will be used in this time is not a commonly stated statistic. On a guess, I would assume a worst case of 1-2 uses in the peak hour, but likely less. However, given I have no data on this and collecting such data would be both intrusive and expensive, I will opt to follow the example of Roy Hunter’s report. That is to say I shall assume a use every five minutes (yes, this is quite high when considered for this application but it is the assumptions which drive the commonly accepted Hunter’s curve sizing). By doing this, I find a probability of 0.07314 (or 7.314%). This is much higher than the values provided for private water closets. Paired with water closets are public lavatories. These, as stated earlier, we can simply look up a flow rate for, and in many places you find this to be a code maximum of 0.5 gpm. Looking at the CDC, we see they recommend 20 seconds of scrubbing for hand washing, so knowing that everyone follows such guidelines to the letter, we shall take that to be our operation time. It is reasonable to assume that whenever someone utilizes a water closet they will also use the lavatory we will give it the same number of uses in the same time (once every five minutes). By these assumptions we can find that public lavatories have a probability of 0.06667 or 6.667%.
WaterDemandCalc_Screen: The IAPMO Water Demand Calculator accurately predicts peak water demand in single-family homes and apartment buildings, reducing the carbon footprint of the structure and saving consumers on both their water and water heating-related energy utility bills for the entire life of the plumbing system. Image courtesy of IAPMO
Stepping out of the bathroom, we may find ourselves in a fitness room, club room or even golf simulator. There are not many plumbing fixtures typically found in these other than perhaps a simple sink or drinking fountain / bottle filler. As the five minute operation period worked so well for the previous fixtures we might as well assume a similar use for these fixtures given our lack of data. Public sinks will typically vary from 0.5 gpm flow rate (for hand sinks) to 1.8 gpm or even 2.2 gpm (for amenity kitchen sinks). How long they should operate for is a greater question.
If they are handwashing sinks, the assumptions for the lavatory can be held and its probability used. Yet, if they are more of a sort of public kitchen sink or laundry sink, then they can be expected to operate for a longer time, say 30 seconds should someone wash dishes after a very early morning party in the club room. As such, by using these assumptions, we would find such amenity kitchen or laundry sinks to have a probability of 0.0999 or 9.999%. Likewise, a bottle filler or drinking fountain may find itself used for a great variety of ranges, but to err on the conservative side, let us say 30 seconds. You will notice that with fixtures like sinks or drinking fountains, their flow rate does not affect their probability, so this will match that of a public kitchen sink. Drinking fountains and bottle fillers however will have much lower flow rates, which will typically be equal to or less than 0.5 gpm.
Let us consider though not only the fancy apartments with common spaces added to raise their rent, but also more affordable projects, which to lower their costs, forgo clothes washers in the units in favor of batteries in common spaces for residents’ use. These units are typically similar to residential units in terms of use and cycle time. As such we can find an operation time by dividing typical water use (19 gallons) by the typical flow rate (3.5 gpm) to find a total draw time over the cycle of 326 seconds. Such batteries of washers tend to experience queuing, so it is best to assume that our T is going to be roughly equal to average cycle time (50 minutes). Combining all this we find a probability of 0.108667 or 10.867%.
Finally, buildings, whether affordable or luxury, may or may not include a janitorial room with things such as a mop sink or have a trash chute which requires a wash down. Trash chutes are actually much simpler than might be expected. They have flow rates around 4 gpm, though this should be checked as they can vary significantly. They are also typically operated for 10 minutes once a week, which if they are operated manually will likely occur during the 8 hour day of a 5 day work week giving a probability of 0.00417 or 0.417% or if operated automatically at any point during the week giving a probability of 0.00099 or 0.099%. This fixture does bring up a certain point, and that is if the probability is less than 1% and has a large flow,, the result of the calculation may be less than the fixture flow rate. If this is the case then the fixture flow rate should be used instead. Mop sinks are harder to predict, but a reasonable worst case is one mop bucket filled in the peak hour. Mop sinks however have another problem, a typical mop sink will have a flow rate of 8 gpm, this is higher than the maximum other fixture input flow rate allowed by the WDC. This is not a technical limitation of the mathematics, but rather a stipulation the program puts on for one reason or another. As such people wishing to calculate mop sinks (or the flush valve fixtures I have included at the end summary table) need to be able to perform the WDCs calculations themselves. How to do that is a very large discussion for another time. A typical mop bucket is 5 gallons, and so a fill time of 38 seconds can be expected. The probability works out to 0.01056 or 1.056%.
Fortunately, while the WDC does not provide much guidance for their use, their calculator does provide three spaces for “other” fixtures. For these, one simply needs a flow rate and a probability. Flow rates are fairly easy to obtain, for faucets typically being stated, and for other fixtures, typical values can be found with a little searching.
Now, you may notice one particular fixture which the WDC does provide a tad bit of guidance for, but is not truly included that I have not yet mentioned. That is the hose bibb. These are scattered throughout almost every apartment building. The WDC calculator user guide recommends to simply add the flow on to the calculated result. On this matter I have slight disagreement. Firstly, as I mentioned, there can be quite a number of these on a building, and with flows often around 4 gpm to add all these would represent an extreme flow. Second, considering their use on apartments, they are unlikely to be used at the same time (being operated only usually by the one or two maintenance personnel). As such, I think it is reasonable that hose bibbs and other infrequently used fixtures, simply find the single fixture of them with the largest flow rate and add that to the calculated flow.
I have included below a summary of the examples I used in this article. It is up to each designer to consider their application and if the assumptions stated here are accurate to the buildings intended use. For clarity of other designers and reviewers, it is best that assumptions such as these be stated either in a table or described in a narrative as there is currently no official standard for these fixtures.
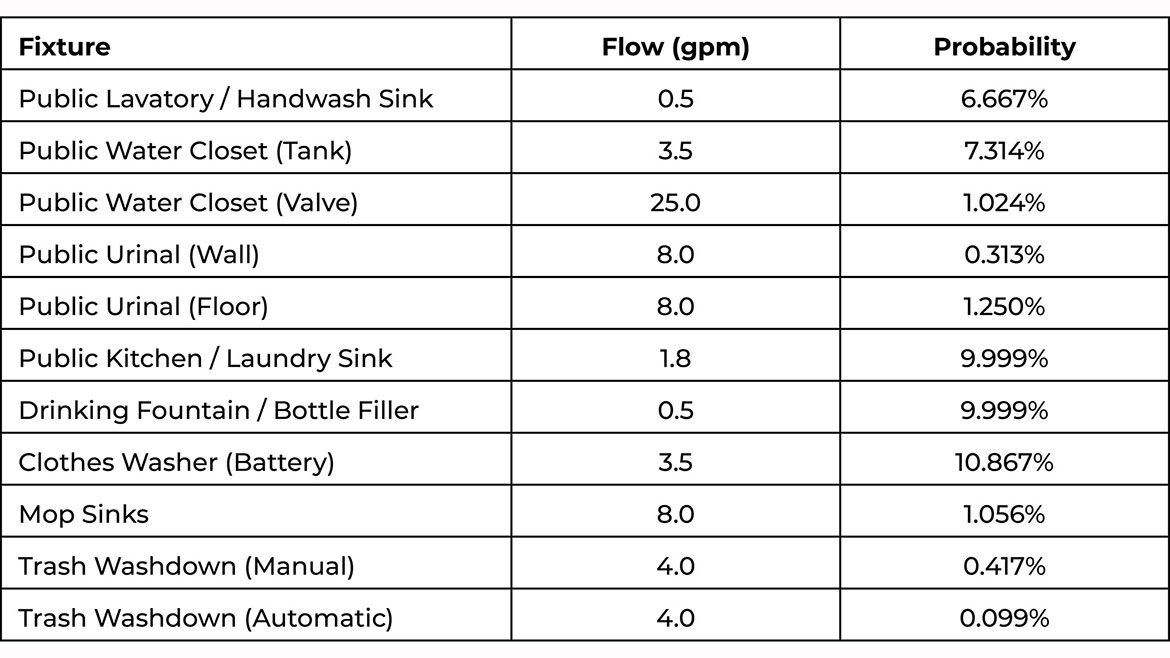
Courtesy of David Beal
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!









