Nature vs. math
Formulas and assumptions don’t always predict what happens.

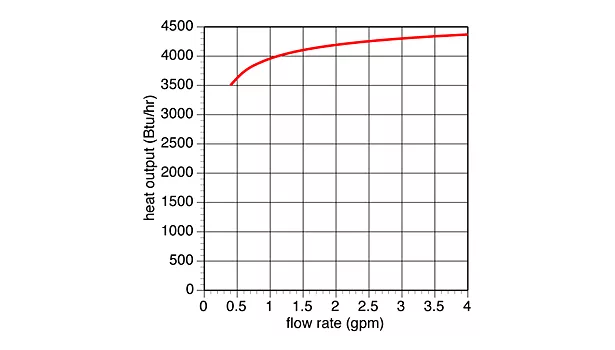
Figure 1.

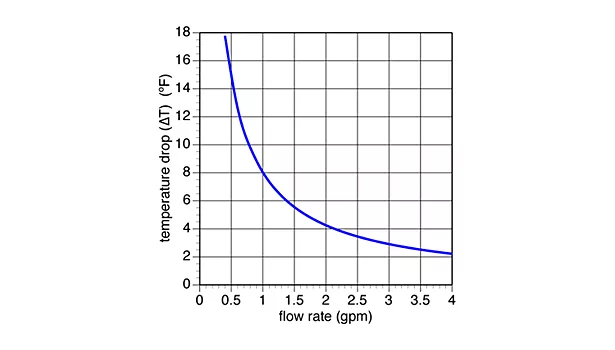
Figure 2.

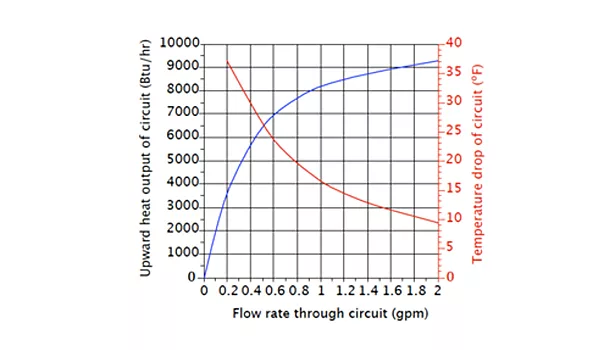
Figure 3.



The following formula has been around the North American hydronics industry for a long time:
Btu/hr. = 500 x gpm x ∆T
It can be used to estimate the rate of heat transfer into or out of a device that has a stream of water flowing through it at a known flow rate, and with a measured temperature change between the inlet and outlet of that water stream.
For example: If a heat emitter is operating at a flow rate of 8 gpm and if the temperature drop from its water inlet to its water outlet was measured to be 20º F, then that stream is delivering heat to the heat emitter at a rate of:
Btu/hr. = 500 x 8 x 20 = 80,000 Btu/hr.
You also could apply this formula to calculate the rate of heat transfer delivered by a stream of water flowing through a heat emitter at 16 gpm and undergoing a temperature drop of 10º.
Btu/hr. = 500 x 16 x 10 = 80,000 Btu/hr.
If you think about the math involved, you probably realize an infinite number of combinations of water flow rate and temperature change exist that would give the same result of 80,000 Btu/hr. Here are just a few:
Btu/hr. = 500 x 32 x 5 = 80,000 Btu/hr.
Btu/hr. = 500 x 160 x 1 = 80,000 Btu/hr.
Btu/hr. = 500 x 80 x 2 = 80,000 Btu/hr.
However, don’t interpret this math to imply that all these combinations are achievable operating conditions. For example, if you assumed a heat emitter could operate with a 800º temperature drop and a flow rate of 0.2 gpm, the math would work out as:
Btu/hr. = 500 x 0.2 x 800 = 80,000 Btu/hr.
But do you really think you could pass water through a hydronic heat emitter at 0.2 gpm and have that water undergo an 800º temperature drop? If so, I suggest you run some tests. If it works, immediately file a patent application on the process, because you’re going to become a billionaire.
Math vs. reality
There is a distinct difference between what the formula (Btu/hr. = 500 x gpm x ∆T) calculates as the rate of heat transfer from measured flow rate and temperature drop values, and how this formula should be used to predict the heat transfer rate from assumed flow rate and temperature drop numbers.
Suppose you designed a distribution system that would operate at a flow rate of 8 gpm and a 20º water temperature drop under design-load conditions. Then you pondered how the system should operate under half-load conditions (e.g., a heat output of 40,000 Btu/hr.). You might assume that by slowing the flow rate from 8 gpm to 4 gpm and maintaining a 20º temperature drop, the system would release half its design-load output. After all, the math works out as follows:
Btu/hr. = 500 x 4 x 20 = 40,000 Btu/hr.
Unfortunately, nature doesn’t agree. To see why, take a look at Figure 1 (page 20), which shows the heat output vs. flow rate relationship for a 12-ft.-long piece of typical residential fin-tube baseboard being supplied with 160º water. The baseboard this graph is based on is rated to release 600 Btu/hr./ft. of element at a 200º water temperature and 1 gpm flow rate.
This graph is based on a detailed engineering model of fin-tube baseboard that accounts for continually decreasing water temperature along the element. The heat output of a 1-in.-long segment of element, at some location along the baseboard, is slightly lower than the output from a 1-in. segment just upstream of that location and slightly higher than a 1-in. segment just downstream of that location.
The model used to construct Figure 1 also is based on information in a baseboard rating standard published by the former IBR (Institute of Boiler & Radiator Manufacturers). Specifically, that heat output varies with the 0.04 power of flow rate. If the heat output from a baseboard at a flow rate of 1 gpm is 250 Btu/hr./ft., then the heat output from that baseboard at a flow rate of 4 gpm (and the same water temperature) would be:
250 x (4)0.04 = 250 x 1.057 = 264 Btu/hr.
If you check heat output tables from baseboard manufacturers, you’ll find this factor of 1.057 is often the ratio between the output number listed for a flow rate of 4 gpm and the output listed for a flow rate of 1 gpm.
Reality vs. assumption
Let’s use Figure 1, starting with a water flow rate of 4 gpm, entering the baseboard at 160º. Room air flows into the fin-tube element at 68º. Under these conditions, the baseboard’s heat output is about 4,350 Btu/hr.
Now look what happens if you maintain the same inlet water temperature and same inlet air temperature, but reduce the flow rate by 50% (e.g., from 4 gpm to 2 gpm). The heat output drops from 4,350 Btu/hr. to about 4,200 Btu/hr. — a drop of only about 3.5%.
If the flow is cut in half again, down to 1 gpm, the heat output drops to about 3,900 Btu/hr., a drop of about 10.3% from the heat output at a 4 gpm flow rate.
The curve in Figure 1 doesn’t go below flow rates of 0.4 gpm. That’s because at flow rates in the range of 0.3 gpm, the water passing through the 3/4-in. copper fin-tube transitions from turbulent to laminar flow. This will cause a significant drop in heat output. But at exactly what flow rate below 0.4 gpm this transition occurs is hard to predict, so this portion of the graph can’t be shown with reasonable certainty.
The take away is that even after reducing the flow rate from 4 gpm to 0.4 gpm, the heat output of the baseboard is still about 3,500 Btu, or roughly 20% lower than at 4 gpm.
Twenty is not a magic number
Figure 2 shows what happens with the temperature drop across the same 12 ft. baseboard as the flow varies across the same range, while the supply water temperature remains at 160º.
At 4 gpm, the temperature drop across this baseboard is only about 2.2º. At 2 gpm, it’s about 4.2º and at 1 gpm, the ∆T is about 8º. If the flow gets down to 0.4 gpm, the ∆T is just under 18º. The takeaway here is that the temperature drop along the baseboard naturally changes as the flow rate through the baseboard changes. The notion that a system “wants to” or even can remain at a fixed temperature drop as the flow rate changes is not supported by these results.
This behavior is not limited to fin-tube baseboard. It also applies to other heat emitters such as fan coils and radiant panel circuits. Figure 3 (page 22) shows what happens with upward heat output and temperature drop for a 300-ft.-long circuit of 1/2-in. PEX tubing buried in a bare 4-in.-thick concrete slab at tube spacing of 12 in. The circuit is supplied with water at 110º. The room temperature above the floor is 70º.
Reducing the flow rate from 2 gpm to 1 gpm only reduces heat output from about 9,300 Btu/hr. to about 8,200 Btu/hr., a drop of about 12%. The corresponding temperature drop along the circuit changes from about 9.5º at 2 gpm to about 17º at 1 gpm.
Don’t assume that just because a mathematical formula is balanced on both sides of the equals sign that nature will “mold itself” to make sure it agrees with the math.
Next month we’ll look at the number 500 in the following formula:
Btu/hr. = 500 x gpm x ∆T
You’ll see where it comes from and that it, too, is subject to change, depending on the fluid used and the temperature at which that fluid operates.
To read the article in pdf form click here.
HELPFUL LINKS:
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!